Soal dan pembahasan gerak lurus berubah beraturan glbb
Soal dan pembahasan soal gerak lurus berubah beraturan glbb
Soal gerak lurus berubah beraturan glbb.
1. Benda yang mula-mula diam dipercepat dengan percepatan 4 m/s2 dan benda menempuh lintasan lurus. Tentukan (a) laju benda pada akhir detik ke 4, (b) jarak yang ditempuh dalam 4 detik (c) laju rata-rata dalam selang waktu 4 detik pertama.
Panduan jawaban :
a) laju benda pada akhir detik ke 4
Diketahui :
vo = 0 m/s (benda mula-mula diam karenanya laju awal = 0 m/s)
a = 4 m/s2
t = 4 s
Ditanya : vt
vt = vo + at = 0 m/s + (4 m/s2)(4 s) = 16 m/s
b) jarak yang ditempuh dalam 4 detik
s = vot + ½ at2 = (0 m/s)(4 s) + ½ (4 m/s2)(4s)2 = 0 + (2 m/s2)( 16 s2) = 32 m
c) laju rata-rata dalam selang waktu 4 detik pertama
2.
Laju sebuah bus bertambah secara teratur dari 20 km/jam menjadi 50
km/jam dalam waktu 10 sekon. Tentukan (a) besar percepatan, (b) jarak
yang ditempuh, (c) laju rata-rata. Nyatakan dalam satuan meter dan
sekon.
Panduan jawaban :
Diketahui :
vo = 20 km/jam = 20 (1000 m) / 3600 s = 5,5 m/s
vt = 50 km/jam = 50 (1000 m) / 3600 s = 13,8 m/s
t = 10 s
a) Besar percepatan
b) jarak yang ditempuh
s = vot + ½ at2 = (5,5 m/s)(10 s) + ½ (0,83 m/s2)(10 s)2
s = 55 m + (0,415 m/s2)(100 s2) = 55 m + 41,5 m
s = 96,5 m
(c) laju rata-rata
3.
Sebuah mobil mula-mula bergerak dengan laju 10 m/s mengurangi lajunya 2
m/s setiap detik. Tentukan jarak yang ditempuh mobil sebelum berhenti.
Panduan jawaban :
Diketahui :
vo = 10 m/s (ini adalah laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini adalah laju akhir mobil)
a = – 2 m/s2 (percepatan diberi tanda negatif karena mobil mengalami perlambatan)
Ditanyakan : jarak tempuh sebelum mobil berhenti (s)
4. Sepeda motor yang sedang bergerak dengan laju 20 m/s mengalami perlambatan hingga dalam waktu 4 sekon lajunya menjadi 5 m/s. Tentukan (a) percepatan sepeda motor, (b) jarak yang ditempuh sepeda motor pada detik kedua.
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal sepeda motor)
vt = 5 m/s (ini laju akhir sepeda motor)
t = 4 s
a) percepatan sepeda motor
Percepatan bernilai negatif karena sepeda motor mengalami perlambatan.
b) jarak yang ditempuh pada detik kedua
s = vot + ½ at2
s = (20 m/s)(2 s) + ½ (-3,75 m/s2)(2 s)2 = 40 m + ½ (-3,75 m/s2)(4 s2)
s = 40 m + (-3,75 m/s2)(2 s2) = 40 m – 7,5 m = 32,5 m
Setelah detik kedua, sepeda motor bergerak sejauh 32,5 meter.
5. Laju mobil berkurang secara teratur dari 20 m/s menjadi 10 m/s dalam jarak 100 meter. Tentukan (a) Besar percepatan mobil, (b) Jika percepatan tetap, hitung jarak yang masih dapat ditempuh mobil sebelum berhenti.
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal mobil)
vt = 10 m/s (ini laju akhir mobil)
s = 100 m
a) Besar percepatan mobil
Mobil mengalami perlambatan karenanya percepatan bernilai negatif.
b) Jika percepatan tetap, hitung jarak yang masih dapat ditempuh mobil sebelum berhenti
Diketahui :
vo = 10 m/s (ini laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini laju akhir mobil)
a = -1,5 m/s2
Ditanyakan : s
Jika mobil mengalami perlambatan konstan maka jarak yang masih dapat ditempuh mobil sebelum berhenti adalah 33,3 meter.
6. Gerak sebuah benda berubah secara beraturan dari kelajuan 4 m/s sampai berhenti. Gambarkan grafik kelajuan (v) terhadap waktu (t) jika jarak yang ditempuhnya mencapai 2 meter.
Panduan jawaban :
Grafik belum bisa digambar karena selang waktu (t) belum diketahui. Terlebih dahulu kita cari selang waktu sebelum benda berhenti.
Diketahui :
vo = 4 m/s (ini laju awal benda)
vt = 0 m/s (ketika benda berhenti, laju benda = 0. Ini laju akhir benda)
s = 2 m
Ditanyakan : t
Berdasarkan data yang diketahui, terlebih dahulu kita hitung besar perlambatan benda.
Dari laju 4 m/s sampai berhenti, mobil bergerak hanya selama 1 sekon Berikut grafiknya…
7. Seorang pengendara mobil yang sedang bergerak dengan laju 80 km/jam, melihat seorang nenek ditengah jalan pada jarak 100 meter di depannya. Jika mobil direm dengan perlambatan maksimum sebesar 2 m/s2, apakah mobil menabrak nenek tersebut ?
Panduan jawaban :
Agar mobil menabrak nenek tersebut maka jarak tempuh mobil setelah perlambatan harus lebih besar atau sama dengan 100 meter. Sebaliknya, jika jarak tempuh mobil kurang dari 100 meter maka nenek tidak tertabrak.
Diketahui :
vo = 80 km/jam = 80 (1000 m) / 3600 s = 22,2 m/s (ini laju awal mobil)
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s. Ini laju akhir mobil)
a = – 2 m/s2 (diberi tanda negatif karena mobil mengalami perlambatan)
Ditanyakan : s
Setelah mengalami perlambatan, mobil masih bergerak sejauh 123,21 meter sebelum berhenti. Berarti nenek tertabraK sopir masuk bui
8. Sebuah mobil dipercepat dari 40 km/jam sampai 60 km/jam, sedangkan mobil lain dipercepat dari keadaan diam sampai 20 km/jam. Jika kedua mobil tersebut dipercepat selama selang waktu yang sama, mobil mana yang memiliki percepatan yang lebih kecil ?
Panduan jawaban :
Selang waktu sama. Kita andaikan selang waktu 1 jam.
Diketahui :
Data mobil 1
vo = 40 km/jam
vt = 60 km/jam
t = 1 jam
Data mobil 2
vo = 0 km/jam (mula-mula mobil diam karenanya laju awal = 0 km/jam).
vt = 20 km/jam
t = 1 jam.
Percepatan mobil 1 :
Ini berarti laju mobil bertambah 20 km/jam setiap 1 jam.
Percepatan mobil 2 :
Besar percepatan kedua mobil sama.
9. Sebuah mobil diperlambat dari 20 m/s sampai berhenti dalam jarak 10 meter. Berapa besar perlambatannya ?
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini laju akhir mobil)
s = 10 m
Ditanyakan : a
Mobil balap kali ya…
10. Sebuah pesawat terbang ringan harus mencapai laju 30 m/s untuk lepas landas. Berapa panjang landasan pacu yang dibutuhkan jika percepatannya adalah 3 m/s2 ?
Panduan jawaban :
Diketahui :
vo = 0 m/s
vt = 30 m/s
a = 3 m/s2
Ditanyakan : s
Panjang landasan pacu minimum = 150 meter
11. Sebuah mobil melambat dari laju 20 m/s sampai berhenti dalam waktu 5 sekon. Berapa jarak yang ditempuhnya dalam waktu itu ?
Panduan jawaban :
Diketahui :
vo = 20 m/s
vt = 0 m/s (ketika mobil berhenti lajunya = 0 m/s. Ini laju akhir mobil)
t = 5 sekon
Ditanyakan = s
Berdasarkan data di atas, terlebih dahulu kita hitung besar perlambatan mobil (a).
Sekarang kita hitung jarak tempuh (s)
s = vot + ½ at2 = (20 m/s)(5 s) + ½ (-4 m/s2)(5 s)2
s = 100 m + (-2 m/s2)(25 s2) = 100 m – 50 m = 50 meter
12. Sebelum berhenti, sebuah mobil meninggalkan bekas sepanjang 40 m di jalan. Dengan menganggap perlambatan 5 m/s2, perkirakan laju mobil tersebut tepat sebelum pengereman.
Panduan jawaban :
Diketahui :
s = 40 m
a = -5 m/s2
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s)
Ditanyakan : vo
13. Sebuah mobil mulai bergerak dari keadaan diam dengan percepatan tetap sebesar 2 m/s2.
Setelah mobil bergerak selama 20 sekon, mesin mobil dimatikan. Jika
mobil berhenti 20 detik kemudian, berapakah jarak yang masih ditempuh
mobil sejak mesinnya dimatikan hingga mobil tersebut berhenti ?
Panduan jawaban :
Terlebih dahulu kita hitung laju mobil ketika mesinnya dimatikan.
Diketahui :
a = 2 m/s2
t = 20 s
vo = 0 m/s (mula-mula mobil diam karenanya laju awalnya = vo = 0 m/s)
vt = vo + at = 0 m/s + (2 m/s2)(20 s) = 40 m/s
Ketika mesinnya dimatikan, mobil bergerak dengan laju 40 m/s
——————————
Sekarang kita hitung jarak yang masih ditempuh mobil setelah mesinnya dimatikan.
Diketahui :
vo = 40 m/s (ini adalah laju awal mobil)
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s. Ini laju akhir mobil)
t = 20 s (mobil berhenti 20 sekon setelah mesinnya dimatikan)
Ditanyakan : s
Menggunakan data di atas, terlebih dahulu kita cari besar perlambatan mobil.
Sekarang kita hitung s :
s = vot + ½ at2 = (40 m/s)(20 s) + ½ (-2 m/s2)(20 s)2
s = 800 m + (-1 m/s2)(400 s2) = 800 m – 400 m = 400 meter
Jarak yang masih ditempuh mobil setelah mesinnya dimatikan = 400 meter
10. Sebuah mobil bergerak dengan percepatan 2m/s2. Setelah berjalan selama 20 s, mesin mobil mati dan berhenti 10 s kemudian. Berapa jarak yang ditempuh oleh mobil tersebut ? (GLBB)
Jawab:
Sebelum mesin mobil mati
Vo = 0
a = 2 m/s2
t = 20 s
Vt = Vo + at
Vt = 0 + 2 . 20
Vt = 40 m/s2
Setelah mesin mobil mati
Vo = 40 m/s2
Vt = 0
t = 10s
Vt = Vo + at
Vt = 40 + a. 10
a = -4
S =Vo t + ½ a t2
S = 40. 10 + ½ (-4) .102
S = 200 m
Jadi, mobil tersebut telah menempuh jarak sejauh 200m sejak mulai bergerak hingga berhenti menempuh jarak 200 m
Soal gerak lurus berubah beraturan glbb.
1. Benda yang mula-mula diam dipercepat dengan percepatan 4 m/s2 dan benda menempuh lintasan lurus. Tentukan (a) laju benda pada akhir detik ke 4, (b) jarak yang ditempuh dalam 4 detik (c) laju rata-rata dalam selang waktu 4 detik pertama.
Panduan jawaban :
a) laju benda pada akhir detik ke 4
Diketahui :
vo = 0 m/s (benda mula-mula diam karenanya laju awal = 0 m/s)
a = 4 m/s2
t = 4 s
Ditanya : vt
vt = vo + at = 0 m/s + (4 m/s2)(4 s) = 16 m/s
b) jarak yang ditempuh dalam 4 detik
s = vot + ½ at2 = (0 m/s)(4 s) + ½ (4 m/s2)(4s)2 = 0 + (2 m/s2)( 16 s2) = 32 m
c) laju rata-rata dalam selang waktu 4 detik pertama
2.
Laju sebuah bus bertambah secara teratur dari 20 km/jam menjadi 50
km/jam dalam waktu 10 sekon. Tentukan (a) besar percepatan, (b) jarak
yang ditempuh, (c) laju rata-rata. Nyatakan dalam satuan meter dan
sekon.Panduan jawaban :
Diketahui :
vo = 20 km/jam = 20 (1000 m) / 3600 s = 5,5 m/s
vt = 50 km/jam = 50 (1000 m) / 3600 s = 13,8 m/s
t = 10 s
a) Besar percepatan
b) jarak yang ditempuh
s = vot + ½ at2 = (5,5 m/s)(10 s) + ½ (0,83 m/s2)(10 s)2
s = 55 m + (0,415 m/s2)(100 s2) = 55 m + 41,5 m
s = 96,5 m
(c) laju rata-rata
3.
Sebuah mobil mula-mula bergerak dengan laju 10 m/s mengurangi lajunya 2
m/s setiap detik. Tentukan jarak yang ditempuh mobil sebelum berhenti.Panduan jawaban :
Diketahui :
vo = 10 m/s (ini adalah laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini adalah laju akhir mobil)
a = – 2 m/s2 (percepatan diberi tanda negatif karena mobil mengalami perlambatan)
Ditanyakan : jarak tempuh sebelum mobil berhenti (s)
4. Sepeda motor yang sedang bergerak dengan laju 20 m/s mengalami perlambatan hingga dalam waktu 4 sekon lajunya menjadi 5 m/s. Tentukan (a) percepatan sepeda motor, (b) jarak yang ditempuh sepeda motor pada detik kedua.
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal sepeda motor)
vt = 5 m/s (ini laju akhir sepeda motor)
t = 4 s
a) percepatan sepeda motor
Percepatan bernilai negatif karena sepeda motor mengalami perlambatan.
b) jarak yang ditempuh pada detik kedua
s = vot + ½ at2
s = (20 m/s)(2 s) + ½ (-3,75 m/s2)(2 s)2 = 40 m + ½ (-3,75 m/s2)(4 s2)
s = 40 m + (-3,75 m/s2)(2 s2) = 40 m – 7,5 m = 32,5 m
Setelah detik kedua, sepeda motor bergerak sejauh 32,5 meter.
5. Laju mobil berkurang secara teratur dari 20 m/s menjadi 10 m/s dalam jarak 100 meter. Tentukan (a) Besar percepatan mobil, (b) Jika percepatan tetap, hitung jarak yang masih dapat ditempuh mobil sebelum berhenti.
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal mobil)
vt = 10 m/s (ini laju akhir mobil)
s = 100 m
a) Besar percepatan mobil
Mobil mengalami perlambatan karenanya percepatan bernilai negatif.b) Jika percepatan tetap, hitung jarak yang masih dapat ditempuh mobil sebelum berhenti
Diketahui :
vo = 10 m/s (ini laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini laju akhir mobil)
a = -1,5 m/s2
Ditanyakan : s
Jika mobil mengalami perlambatan konstan maka jarak yang masih dapat ditempuh mobil sebelum berhenti adalah 33,3 meter.
6. Gerak sebuah benda berubah secara beraturan dari kelajuan 4 m/s sampai berhenti. Gambarkan grafik kelajuan (v) terhadap waktu (t) jika jarak yang ditempuhnya mencapai 2 meter.
Panduan jawaban :
Grafik belum bisa digambar karena selang waktu (t) belum diketahui. Terlebih dahulu kita cari selang waktu sebelum benda berhenti.
Diketahui :
vo = 4 m/s (ini laju awal benda)
vt = 0 m/s (ketika benda berhenti, laju benda = 0. Ini laju akhir benda)
s = 2 m
Ditanyakan : t
Berdasarkan data yang diketahui, terlebih dahulu kita hitung besar perlambatan benda.
Dari laju 4 m/s sampai berhenti, mobil bergerak hanya selama 1 sekon Berikut grafiknya…7. Seorang pengendara mobil yang sedang bergerak dengan laju 80 km/jam, melihat seorang nenek ditengah jalan pada jarak 100 meter di depannya. Jika mobil direm dengan perlambatan maksimum sebesar 2 m/s2, apakah mobil menabrak nenek tersebut ?
Panduan jawaban :
Agar mobil menabrak nenek tersebut maka jarak tempuh mobil setelah perlambatan harus lebih besar atau sama dengan 100 meter. Sebaliknya, jika jarak tempuh mobil kurang dari 100 meter maka nenek tidak tertabrak.
Diketahui :
vo = 80 km/jam = 80 (1000 m) / 3600 s = 22,2 m/s (ini laju awal mobil)
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s. Ini laju akhir mobil)
a = – 2 m/s2 (diberi tanda negatif karena mobil mengalami perlambatan)
Ditanyakan : s
Setelah mengalami perlambatan, mobil masih bergerak sejauh 123,21 meter sebelum berhenti. Berarti nenek tertabraK sopir masuk bui8. Sebuah mobil dipercepat dari 40 km/jam sampai 60 km/jam, sedangkan mobil lain dipercepat dari keadaan diam sampai 20 km/jam. Jika kedua mobil tersebut dipercepat selama selang waktu yang sama, mobil mana yang memiliki percepatan yang lebih kecil ?
Panduan jawaban :
Selang waktu sama. Kita andaikan selang waktu 1 jam.
Diketahui :
Data mobil 1
vo = 40 km/jam
vt = 60 km/jam
t = 1 jam
Data mobil 2
vo = 0 km/jam (mula-mula mobil diam karenanya laju awal = 0 km/jam).
vt = 20 km/jam
t = 1 jam.
Percepatan mobil 1 :
Ini berarti laju mobil bertambah 20 km/jam setiap 1 jam.Percepatan mobil 2 :
Besar percepatan kedua mobil sama.9. Sebuah mobil diperlambat dari 20 m/s sampai berhenti dalam jarak 10 meter. Berapa besar perlambatannya ?
Panduan jawaban :
Diketahui :
vo = 20 m/s (ini laju awal mobil)
vt = 0 m/s (ketika mobil berhenti, lajunya = 0 m/s. Ini laju akhir mobil)
s = 10 m
Ditanyakan : a
Mobil balap kali ya…10. Sebuah pesawat terbang ringan harus mencapai laju 30 m/s untuk lepas landas. Berapa panjang landasan pacu yang dibutuhkan jika percepatannya adalah 3 m/s2 ?
Panduan jawaban :
Diketahui :
vo = 0 m/s
vt = 30 m/s
a = 3 m/s2
Ditanyakan : s
Panjang landasan pacu minimum = 150 meter11. Sebuah mobil melambat dari laju 20 m/s sampai berhenti dalam waktu 5 sekon. Berapa jarak yang ditempuhnya dalam waktu itu ?
Panduan jawaban :
Diketahui :
vo = 20 m/s
vt = 0 m/s (ketika mobil berhenti lajunya = 0 m/s. Ini laju akhir mobil)
t = 5 sekon
Ditanyakan = s
Berdasarkan data di atas, terlebih dahulu kita hitung besar perlambatan mobil (a).
Sekarang kita hitung jarak tempuh (s)
s = vot + ½ at2 = (20 m/s)(5 s) + ½ (-4 m/s2)(5 s)2
s = 100 m + (-2 m/s2)(25 s2) = 100 m – 50 m = 50 meter
12. Sebelum berhenti, sebuah mobil meninggalkan bekas sepanjang 40 m di jalan. Dengan menganggap perlambatan 5 m/s2, perkirakan laju mobil tersebut tepat sebelum pengereman.
Panduan jawaban :
Diketahui :
s = 40 m
a = -5 m/s2
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s)
Ditanyakan : vo
13. Sebuah mobil mulai bergerak dari keadaan diam dengan percepatan tetap sebesar 2 m/s2.
Setelah mobil bergerak selama 20 sekon, mesin mobil dimatikan. Jika
mobil berhenti 20 detik kemudian, berapakah jarak yang masih ditempuh
mobil sejak mesinnya dimatikan hingga mobil tersebut berhenti ?Panduan jawaban :
Terlebih dahulu kita hitung laju mobil ketika mesinnya dimatikan.
Diketahui :
a = 2 m/s2
t = 20 s
vo = 0 m/s (mula-mula mobil diam karenanya laju awalnya = vo = 0 m/s)
vt = vo + at = 0 m/s + (2 m/s2)(20 s) = 40 m/s
Ketika mesinnya dimatikan, mobil bergerak dengan laju 40 m/s
——————————
Sekarang kita hitung jarak yang masih ditempuh mobil setelah mesinnya dimatikan.
Diketahui :
vo = 40 m/s (ini adalah laju awal mobil)
vt = 0 m/s (ketika berhenti, laju mobil = 0 m/s. Ini laju akhir mobil)
t = 20 s (mobil berhenti 20 sekon setelah mesinnya dimatikan)
Ditanyakan : s
Menggunakan data di atas, terlebih dahulu kita cari besar perlambatan mobil.
Sekarang kita hitung s :
s = vot + ½ at2 = (40 m/s)(20 s) + ½ (-2 m/s2)(20 s)2
s = 800 m + (-1 m/s2)(400 s2) = 800 m – 400 m = 400 meter
Jarak yang masih ditempuh mobil setelah mesinnya dimatikan = 400 meter
10. Sebuah mobil bergerak dengan percepatan 2m/s2. Setelah berjalan selama 20 s, mesin mobil mati dan berhenti 10 s kemudian. Berapa jarak yang ditempuh oleh mobil tersebut ? (GLBB)
Jawab:
Sebelum mesin mobil mati
Vo = 0
a = 2 m/s2
t = 20 s
Vt = Vo + at
Vt = 0 + 2 . 20
Vt = 40 m/s2
Setelah mesin mobil mati
Vo = 40 m/s2
Vt = 0
t = 10s
Vt = Vo + at
Vt = 40 + a. 10
a = -4
S =Vo t + ½ a t2
S = 40. 10 + ½ (-4) .102
S = 200 m
Jadi, mobil tersebut telah menempuh jarak sejauh 200m sejak mulai bergerak hingga berhenti menempuh jarak 200 m
11. Sebuah
lokomotif mula-mula diam, kemudian bergerak dengan percepatan 2 m/s2.
Berapa lama waktu yang dibutuhkan ketika lokomotif menempuh jarak 900 m?
(GLBB)
Jawab :
Harga a = konstan, berarti benda melakukan gerak GLBB
Diketahui : Vo = 0 (diam)
S = 900 m
a = 2 m/2 S = Vo. t + ½ a.t2
900 = 0 + ½ (2). t2
t2 = 900
t = 30 sekon
12. Kereta api Ladoya bergerak lurus beraturan pada rel lurus yogya-bandung sejauh 5 km dalam selang waktu 5 menit. (a) Hitunglah kecepatan kereta (b) berapa lama kereta itu menempuh jarak 50 km ?
Jawab :
(a) Pada soal di atas, diketahui perpindahan (s) = 5 km dan waktu tempuh (t) = 4 menit. Sebelum menghitung kecepatan, kita harus mengkonversi satuan sehingga sesuai dengan Sistem Internasional (SI). Terserah, mana yang ingin dikonversi, ubah menit ke jam atau km di ubah ke meter dan menit di ubah ke detik.
Misalnya yang di ubah adalah satuan menit, maka 4 menit = 0,07 jam.
Ingat bahwa pada GLB, kecepatan benda sama setiap saat, demikian juga dengan kecepatan rata-rata.
v = s / t = 5 km / 0,07 jam = 75 km/jam
(b) Untuk menghitung waktu, persamaan kecepatan di atas dibalik
t = s / v = 50 km / 75 km/jam = 0,67 jam = 40 menit.
Jawab :
Harga a = konstan, berarti benda melakukan gerak GLBB
Diketahui : Vo = 0 (diam)
S = 900 m
a = 2 m/2 S = Vo. t + ½ a.t2
900 = 0 + ½ (2). t2
t2 = 900
t = 30 sekon
12. Kereta api Ladoya bergerak lurus beraturan pada rel lurus yogya-bandung sejauh 5 km dalam selang waktu 5 menit. (a) Hitunglah kecepatan kereta (b) berapa lama kereta itu menempuh jarak 50 km ?
Jawab :
(a) Pada soal di atas, diketahui perpindahan (s) = 5 km dan waktu tempuh (t) = 4 menit. Sebelum menghitung kecepatan, kita harus mengkonversi satuan sehingga sesuai dengan Sistem Internasional (SI). Terserah, mana yang ingin dikonversi, ubah menit ke jam atau km di ubah ke meter dan menit di ubah ke detik.
Misalnya yang di ubah adalah satuan menit, maka 4 menit = 0,07 jam.
Ingat bahwa pada GLB, kecepatan benda sama setiap saat, demikian juga dengan kecepatan rata-rata.
v = s / t = 5 km / 0,07 jam = 75 km/jam
(b) Untuk menghitung waktu, persamaan kecepatan di atas dibalik
t = s / v = 50 km / 75 km/jam = 0,67 jam = 40 menit.
13. Setelah
dihidupkan, Sebuah mobil bergerak dengan percepatan 2m/s2. Setelah
berjalan selama 20 s, mesin mobil mati dan berhenti 10 s kemudian.
Berapa jarak yang ditempuh oleh mobil tersebut ? (GLBB)
Jawab :
Sebelum mesin mobil mati
Vo = 0
a = 2 m/s2
t = 20 s
Vt = Vo + at
Vt = 0 + 2 . 20
Vt = 40 m/s2
Setelah mesin mobil mati
Vo = 40 m/s2
Vt = 0
t = 10s
Vt = Vo + at
Vt = 40 + a. 10
a = -4
S =Vo t + ½ a t2
S = 40. 10 + ½ (-4) .102
S = 200 m
Jadi, mobil tersebut telah menempuh jarak sejauh 200m sejak mulai bergerak hingga berhenti menempuh jarak 200 m
14. Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.
Jika percepatan gravitasi ditempat tersebut adalah 10 m/s2, dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah
Jawab:
a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:
b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:
c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
Jawab :
Sebelum mesin mobil mati
Vo = 0
a = 2 m/s2
t = 20 s
Vt = Vo + at
Vt = 0 + 2 . 20
Vt = 40 m/s2
Setelah mesin mobil mati
Vo = 40 m/s2
Vt = 0
t = 10s
Vt = Vo + at
Vt = 40 + a. 10
a = -4
S =Vo t + ½ a t2
S = 40. 10 + ½ (-4) .102
S = 200 m
Jadi, mobil tersebut telah menempuh jarak sejauh 200m sejak mulai bergerak hingga berhenti menempuh jarak 200 m
14. Batu bermassa 200 gram dilempar lurus ke atas dengan kecepatan awal 50 m/s.
Jika percepatan gravitasi ditempat tersebut adalah 10 m/s2, dan gesekan udara diabaikan, tentukan :
a) Tinggi maksimum yang bisa dicapai batu
b) Waktu yang diperlukan batu untuk mencapai ketinggian maksimum
c) Lama batu berada diudara sebelum kemudian jatuh ke tanah
Jawab:
a) Saat batu berada di titik tertinggi, kecepatan batu adalah nol dan percepatan yang digunakan adalah percepatan gravitasi. Dengan rumus GLBB:
b) Waktu yang diperlukan batu untuk mencapai titik tertinggi:
c) Lama batu berada di udara adalah dua kali lama waktu yang diperlukan untuk mencapai titik tertinggi.
t = (2)(5) = 10 sekon
15. Sebuah
mobil bergerak dengan kelajuan awal 72 km/jam kemudian direm hingga
berhenti pada jarak 8 meter dari tempat mulainya pengereman. Tentukan
nilai perlambatan yang diberikan pada mobil tersebut!
Pembahasan
Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:
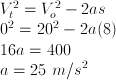
16. Perhatikan grafik berikut ini.
Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.
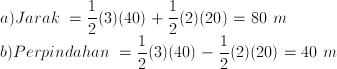
17. Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.
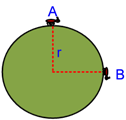
Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
Pembahasan
Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak = 1/4 (2πr) = 1/4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 22 + 22 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
17. Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.
Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
Pembahasan
Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR
PQ = VPQ x tPQ = (200 km/jam) x (0,5) jam = 100 km
QR = VQR x tQR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53o = (100 km) x (0,6) = 60 km
RR' = QR sin 53o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )2 + (RR')2 ]
PR = √[ (160 ) 2 + (80)2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
18. Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:
Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
Pembahasan
Mencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) = 2/3 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) = 3/2 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
19. Dari gambar berikut :
Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasan
a) Jarak tempuh dari A - B
Cara Pertama
Data :
Vo = 0 m/s
a = (2 − 0) : (3− 0) = 2/3 m/s2
t = 3 sekon
S = Vo t + 1/2 at2
S = 0 + 1/2 (2/3 )(3)2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
Vo = 2 m/s
a = 3/2 m/s2
t = 9 − 7 = 2 sekon
S = Vo t + 1/2 at2
S = (2)(2) + 1/2 (3/2 )(2)2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
20. Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.
Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing VA = 40 m/s dan VB = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)
tA = tB
SA/VA = SB/VB
( x )/40 = ( 1200 − x ) /60
6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = VA t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
SB =VB t = (60) (12) = 720 m
21. Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.
Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
Jawab :
Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s2
Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
SA = SB
VA t =VoB t + 1/2 at2
80t = (0)t + 1/2 (4)t2
2t2 − 80t = 0
t2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
SA = VA t = (80)(40) = 3200 meter
Pembahasan
Ubah dulu satuan km/jam menjadi m/s kemudian gunakan persamaan untuk GLBB diperlambat:
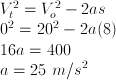
16. Perhatikan grafik berikut ini.
Dari grafik diatas tentukanlah:
a. jarak tempuh gerak benda dari t = 5 s hingga t = 10 s
b. perpindahan benda dari t = 5 s hingga t = 10 s
Pembahasan
Jika diberikan graik V (kecepatan) terhadap t (waktu) maka untuk mencari jarak tempuh atau perpindahan cukup dari luas kurva grafik V-t. Dengan catatan untuk jarak, semua luas bernilai positif, sedang untuk menghitung perpindahan, luas diatas sumbu t bernilai positif, di bawah bernilai negatif.
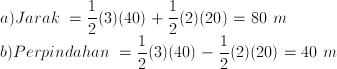
17. Seekor semut bergerak dari titik A menuju titik B pada seperti terlihat pada gambar berikut.
Jika r = 2 m, dan lama perjalanan semut adalah 10 sekon tentukan:
a) Kecepatan rata-rata gerak semut
b) Kelajuan rata-rata gerak semut
Pembahasan
Terlebih dahulu tentukan nilai perpindahan dan jarak si semut :
Jarak yang ditempuh semut adalah dari A melalui permukaan lengkung hingga titik B, tidak lain adalah seperempat keliling lingkaran.
Jarak = 1/4 (2πr) = 1/4 (2π x 2) = π meter
Perpindahan semut dilihat dari posisi awal dan akhirnya , sehingga perpindahan adalah dari A tarik garis lurus ke B. Cari dengan phytagoras.
Perpindahan = √ ( 22 + 22 ) = 2√2 meter.
a) Kecepatan rata-rata = perpindahan : selang waktu
Kecepatan rata-rata = 2√2 meter : 10 sekon = 0,2√2 m/s
b) Kelajuan rata-rata = jarak tempuh : selang waktu
Kelajuan rata- rata = π meter : 10 sekon = 0,1 π m/s
17. Pesawat Burung Dara Airlines berangkat dari kota P menuju arah timur selama 30 menit dengan kecepatan konstan 200 km/jam. Dari kota Q berlanjut ke kota R yang terletak 53o terhadap arah timur ditempuh selama 1 jam dengan kecepatan konstan 100 km/jam.
Tentukan:
a) Kecepatan rata-rata gerak pesawat
b) Kelajuan rata-rata gerak pesawat
Pembahasan
Salah satu cara :
Terlebih dahulu cari panjang PQ, QR, QR', RR', PR' dan PR
PQ = VPQ x tPQ = (200 km/jam) x (0,5) jam = 100 km
QR = VQR x tQR = (100 km/jam) x (1 jam) = 100 km
QR' = QR cos 53o = (100 km) x (0,6) = 60 km
RR' = QR sin 53o = (100 km) x (0,8) = 80 km
PR' = PQ + QR' = 100 + 60 = 160 km
PR = √[ (PR' )2 + (RR')2 ]
PR = √[ (160 ) 2 + (80)2 ] = √(32000) = 80√5 km
Jarak tempuh pesawat = PQ + QR = 100 + 100 = 200 km
Perpindahan pesawat = PR = 80√5 km
Selang waktu = 1 jam + 0,5 jam = 1,5 jam
a) Kecepatan rata-rata = perpindahan : selang waktu = 80√5 km : 1,5 jam = 53,3 √5 km/jam
b) Kelajuan rata-rata = jarak : selang waktu = 200 km : 1,5 jam = 133,3 km/jam
18. Diberikan grafik kecepatan terhadap waktu seperti gambar berikut:
Tentukan besar percepatan dan jenis gerak dari:
a) A - B
b) B - C
c) C - D
Pembahasan
Mencari percepatan (a) jika diberikan grafik V-t :
a = tan θ
dengan θ adalah sudut kemiringan garis grafik terhadap horizontal dan tan suatu sudut adalah sisi depan sudut dibagi sisi samping sudut. Ingat : tan-de-sa
a) A - B
a = (2 − 0) : (3− 0) = 2/3 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
b) B - C
a = 0 (garis lurus, benda bergerak lurus beraturan / GLB)
c) C - D
a = (5 − 2) : (9 − 7) = 3/2 m/s2
(benda bergerak lurus berubah beraturan / GLBB dipercepat)
19. Dari gambar berikut :
Tentukan:
a) Jarak tempuh dari A - B
b) Jarak tempuh dari B - C
c) Jarak tempuh dari C - D
d) Jarak tempuh dari A - D
Pembahasan
a) Jarak tempuh dari A - B
Cara Pertama
Data :
Vo = 0 m/s
a = (2 − 0) : (3− 0) = 2/3 m/s2
t = 3 sekon
S = Vo t + 1/2 at2
S = 0 + 1/2 (2/3 )(3)2 = 3 meter
Cara Kedua
Dengan mencari luas yang terbentuk antara titik A, B dang angka 3 (Luas Segitiga = setengah alas x tinggi) akan didapatkan hasil yang sama yaitu 3 meter
b) Jarak tempuh dari B - C
Cara pertama dengan Rumus GLB
S = Vt
S = (2)(4) = 8 meter
Cara kedua dengan mencari luas yang terbentuk antara garis B-C, angka 7 dan angka 3 (luas persegi panjang)
c) Jarak tempuh dari C - D
Cara Pertama
Data :
Vo = 2 m/s
a = 3/2 m/s2
t = 9 − 7 = 2 sekon
S = Vo t + 1/2 at2
S = (2)(2) + 1/2 (3/2 )(2)2 = 4 + 3 = 7 meter
Cara kedua dengan mencari luas yang terbentuk antara garis C-D, angka 9 dan angka 7 (luas trapesium)
S = 1/2 (jumlah sisi sejajar) x tinggi
S = 1/2 (2+5)(9-7) = 7 meter.
d) Jarak tempuh dari A - D
Jarak tempuh A-D adalah jumlah dari jarak A-B, B-C dan C-D
20. Mobil A dan B dalam kondisi diam terpisah sejauh 1200 m.
Kedua mobil kemudian bergerak bersamaan saling mendekati dengan kecepatan konstan masing-masing VA = 40 m/s dan VB = 60 m/s.
Tentukan:
a) Jarak mobil A dari tempat berangkat saat berpapasan dengan mobil B
b) Waktu yang diperlukan kedua mobil saling berpapasan
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
Pembahasan
Waktu tempuh mobil A sama dengan waktu tempuh mobil B, karena berangkatnya bersamaan. Jarak dari A saat bertemu misalkan X, sehingga jarak dari B (1200 − X)
tA = tB
SA/VA = SB/VB
( x )/40 = ( 1200 − x ) /60
6x = 4( 1200 − x )
6x = 4800 − 4x
10x = 4800
x = 480 meter
b) Waktu yang diperlukan kedua mobil saling berpapasan
x = VA t
480 = 40t
t = 12 sekon
c) Jarak mobil B dari tempat berangkat saat berpapasan dengan mobil A
SB =VB t = (60) (12) = 720 m
21. Diberikan grafik kecepatan terhadap waktu dari gerak dua buah mobil, A dan B.
Tentukan pada jarak berapakah mobil A dan B bertemu lagi di jalan jika keduanya berangkat dari tempat yang sama!
Jawab :
Analisa grafik:
Jenis gerak A → GLB dengan kecepatan konstan 80 m/s
Jenis gerak B → GLBB dengan percepatan a = tan α = 80 : 20 = 4 m/s2
Kedua mobil bertemu berarti jarak tempuh keduanya sama, misal keduanya bertemu saat waktu t
SA = SB
VA t =VoB t + 1/2 at2
80t = (0)t + 1/2 (4)t2
2t2 − 80t = 0
t2 − 40t = 0
t(t − 40) = 0
t = 0 sekon atau t = 40 sekon
Kedua mobil bertemu lagi saat t = 40 sekon pada jarak :
SA = VA t = (80)(40) = 3200 meter
Url Artikel :http://file-education.blogspot.com/2011/10/soal-dan-pembahasan-gerak-lurus-berubah.html
Bergabung Menjadi Anggota Blog:
Berlanganan Artikel Kami Via E-mail:
thanks brow
BalasHapus